Solvolysis of the salt of a weak acid and a weak base

Objective:

1. To determine the extent of solvolysis of ammonium borate in water by calorimeter

Results and calculation:

Part I: Mixture of sodium hydroxide, NaOH and hydrochloric acid, HCl

Table 1.1 The temperature of mixture and the time taken from beginning

Time taken from beginning, t (s)	Temperature, T (°C)
0.0	26.0
0.5	27.0
3.5	28.0
5.5	28.5
7.5	29.0
10.5	29.0
12.0	29.5
14.5	29.5
16.5	29.5
19.5	30.0
22.0	30.0
25.0	30.0
29.5	30.0
32.0	30.0
34.0	30.0
94.0	30.0
154.0	30.0
214.0	30.0
274.0	30.0
324.0	30.0

Graph 1 Temperature of mixture against time taken from beginning

Table 1.2 Temperature change of mixture caused by neutralization reaction

 

Initial temperature, Ti (°C)	26.0
Final temperature, Tf (°C)	30.0
Change of temperature, ΔT (°C)	4.0

 

Part II: Mixture of sodium hydroxide, NaOH and boric acid, H₃BO₃

Table 2.1 The temperature of mixture and the time taken from beginning

 

Time taken from beginning, t (s)	Temperature, T (°C)
0.0	26.0
5.5	27.0
8.5	28.0
13.0	28.0
14.0	28.0
15.0	28.0
24.0	28.5
32.0	29.0
44.5	29.0
58.0	29.0
62.0	29.0
69.0	29.0
129.0	29.0
189.0	29.0
249.0	29.0
309.0	29.0
369.0	29.0

Graph 2 Temperature of mixture against time taken from beginning

Table 2.2 Temperature change of mixture caused by neutralization reaction

Initial temperature, Ti (°C)	26.0
Final temperature, Tf (°C)	29.0
Change of temperature, ΔT (°C)	3.0

Part III: Mixture of ammonia, NH₄OH and hydrochloric acid, HCl

Table 3.1 The temperature of mixture and the time taken from beginning

Time taken from beginning, t (s)	Temperature, T (°C)
0.0	25.0
2.0	26.5
5.0	27.0
6.0	28.5
8.0	29.0
10.5	29.0
12.5	29.0
15.0	29.0
17.5	29.5
20.0	29.5
23.0	29.5
26.0	30.0
29.5	30.0
33.0	30.0
39.0	30.0
99.0	30.0
159.0	30.0
219.0	30.0
279.0	30.0
339.0	30.0

Graph 3 Temperature of mixture against time taken from beginning

Table 3.2 Temperature change of mixture caused by neutralization reaction

Initial temperature, Ti (°C)	25.0
Final temperature, Tf (°C)	30.0
Change of temperature, ΔT (°C)	5.0

Part IV: Mixture of ammonia, NH₄OH and boric acid, H₃BO₃

Table 4.1 The temperature of mixture and the time taken from beginning

Time taken from beginning, t (s)	Temperature, T (°C)
0.0	25.0
3.5	26.0
7.0	27.0
11.5	27.0
15.5	27.0
18.0	27.0
22.5	27.0
27.5	27.0
33.0	27.0
37.5	27.0
42.0	27.0
47.5	27.0
52.5	27.0
88.0	27.0
148.0	27.0
208.0	27.0
268.0	27.0
328.0	27.0

Graph 4 Temperature of mixture against time taken from beginning

Table 4.2 Temperature change of mixture caused by neutralization reaction

Initial temperature, Ti (°C)	25.0
Final temperature, Tf (°C)	27.0
Change of temperature, ΔT (°C)	2.0

 

Determination of limiting agent in each part

In the reaction for part I, the limiting agent is calculated as shown below:

Therefore, limiting agent in the reaction is NaOH solution.

The limiting agent in each part is determined by using the method as shown in Part I.

Determination of heat capacity of calorimeter

From the enthalpy change, it can be expressed in the term of

-q = (m_solution)(c_solution)(ΔT) + (c_calorimeter )( ΔT)

-(-ΔH )(n) = (m_solution)(c_solution)(ΔT) + (c_calorimeter )( ΔT)

Since -ΔH = -q / n, and ΔH is negative because neutralization is an exothermic reaction.

Assumptions:

Specific heat capacity of calorimeter = 1.0 cal °C^-1 g^-1

Density of solution = 1g cm^-3 (125ml solution = 125g solution)

Part I

In part I, the enthalpy change of a strong base and a strong acid is -13.36 kcal mol^-1.

Number of moles of reaction = 0.04375 mol since limiting agent has 0.04375 mol.

Let ΔH₁ be the enthalpy change of neutralization reaction of part I.

-(-ΔH₁ )(n) = (m_solution)(c_solution)(ΔT) + (c_calorimeter )( ΔT)

-(-13.36x10³ cal mol^-1)(0.04375mol) = (125g)( 1.0 cal °C^-1 g^-1)(4°C) + (c_calorimeter )(4°C)

c_calorimeter = 21.125g °C^-1

Determination of enthalpy change of each reaction

Part II

Based on part I, c_calorimeter = 21.125 cal °C^-1, ΔT = 3°C

Number of moles of reaction = 0.04375 mol since limiting agent has 0.04375 mol.

Let ΔH₂ be the enthalpy change of neutralization reaction of part II.

-(-ΔH₂ )(n) = (m_solution)(c_solution)(ΔT) + (c_calorimeter )( ΔT)

-(-ΔH₂)(0.04375mol) = (125g)( 1.0 cal °C^-1 g^-1)(3°C) + (21.125 cal °C^-1)(3°C)

ΔH₂ = 10.02 kcal mol^-1

Since neutralization is an exothermic process, so ΔH₂ = -10.02 kcal mol^-1.

Part III

Based on part I, c_calorimeter = 21.125 cal °C^-1, ΔT = 5°C

Number of moles of reaction = 0.04375 mol since limiting agent has 0.04375 mol.

Let ΔH₃ be the enthalpy change of neutralization reaction of part III.

-(-ΔH₃ )(n) = (m_solution)(c_solution)(ΔT) + (c_calorimeter )( ΔT)

-(- ΔH₃)(0.04375mol) = (125g)( 1.0 cal °C^-1 g^-1)(5°C) + (21.125 cal °C^-1)(5°C)

ΔH₃ = 16.7 kcal mol^-1

Since neutralization is an exothermic process, so ΔH₃ = -16.7 kcal mol^-1. However, this value is not valid due to certain error. The enthalpy change of the neutralization reaction between a weak base and a strong acid should be less than the reaction between strong acid and strong base.

Part IV

Based on part I, c_calorimeter = 21.125 cal °C^-1, ΔT = 2°C

Number of moles of reaction = 0.04375 mol since limiting agent has 0.04375 mol.

Let ΔH₄ be the enthalpy change of neutralization reaction of part IV.

-(-ΔH₄ )(n) = (m_solution)(c_solution)(ΔT) + (c_calorimeter )( ΔT)

-(- ΔH₄)(0.04375mol) = (125g)( 1.0 cal °C^-1 g^-1)(2°C) + (21.125 cal °C^-1)(2°C)

ΔH₄ = 6.68 kcal mol^-1

Since neutralization is an exothermic process, so ΔH₄ = -6.68 kcal mol^-1.

Determination of enthalpy change of dissociation of H₃BO₃ and NH₃

Assumption: The reaction between weak base and weak acid goes to completion.

By using the ΔH’s value of obtained,

ΔH₄ = ΔH₂ + ΔH₃ – ΔH₁

ΔH₄ = -10.02 kcal mol^-1 + (-16.7 kcal mol^-1) – (-13.36kcal mol^-1)

ΔH₄ = -13.36 kcal mol^-1

The enthalpy change of neutralization between a weak base and a weak acid is -13.36 kcal mol^-1. By comparing to the value calculated, ΔH₄ = -6.68 kcal mol^-1 (from part IV), this value is bigger. According to the reaction between weak base and weak acid, this value is not valid because the expected value should be less than the value obtained in part I, part II and part III. Since the value of ΔH₃ is not valid, therefore the value obtained by using ΔH₄ = ΔH₂ + ΔH₃ – ΔH₁ is no longer valid.

Determination of fraction of the salt ammonium borate reacts with water

Let a be the fraction of ammonium borate salt reacts with water

K_solv = equilibrium constant of solvolysis

a = 1 – a’ = 1 – (ΔH / ΔH₄)

K = a² / (1-a)²

Based on the formula given above, the fraction of ammonium borate salt reacts with water and equilibrium constant of solvolysis were calculated in each part.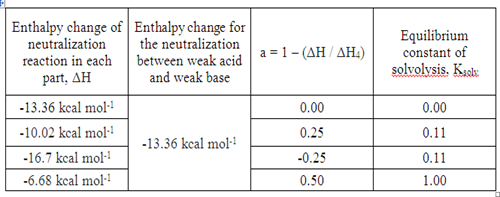

For ΔH = -16.7 kcal mol^-1, the value of fraction of the salt ammonium borate reacts with water is negative value which is -0.25. This is an invalid value. Hence, the value of equilibrium constant of solvolysis is not valid too.

Determination of the dissociation constant, K_a for boric acid

From the previous part, the equilibrium constant of solvolysis for part IV is 1.00, and the value of K_w = 1.0 x 10^-14 and K_b = 1.75 x 10^-5. Therefore, the value of K_a of boric acid is calculated as shown below:

1.00 = 1.0 x 10^-14 / (K_a)(1.75 x 10^-5)

K_a = 5.71 x 10^-10

According to the journal article, Perelygin, Yu. P. & D. Yu. Chistyakov (2006). Boric acid. Russian Journal of Applied Chemistry, 79(12), 2041-2042. doi: 10.1134/S1070427206120305. (Dissociation constant of K_a is 7.3 x 10^-10)

The value obtained experimentally is 5.71 x 10^-10 which shows a deviation with the value of K_a obtained via journal article.