Objective:
1. To study the thermodynamics of solubility of naphthalene in dipheylamine
2. To determine the molal freezing point depression constant of naphthalene
Introduction:
Solubility is the ability of a substance to dissolve in water. The solubility is measured in terms of concentration of an ion that is present in a smaller ratio in solution. On the other hand, solubility equilibrium refers to the equilibrium between the dissolved salt (ions) and undissolved salt that usually exists in a saturated solution or a solution of a sparingly soluble salt.
Naphthalene (pure solid) Naphthalene (solution, mole fraction on X)
The reaction we shall study is the solubility of naphthalene, C10H8 in diphenylamine, C12H11N, which can be written as the equation shown above. For a saturated solution, the equilibrium constant for this reaction is
K =
Since the activity of a pure solid is unity, so
aNaphthalene (solid)= 1
Assuming that the solution is ideal solution, the activity of naphthalene in the solution is equals to its mole fraction in which aNaphthalene (solution) = X. Therefore, the equilibrium constant is K =X. By the argument of the preceding section, we should predict that the temperature dependence of this solubility equilibrium would be:
= =- [ - ]
The temperature dependence of this equilibrium if found by determining the temperature at which naphthalene first precipitates from liquid mixtures of naphthalene and diphenylamine. This is the temperature at which the mole fraction X in naphthalene solution is saturated with naphthalene. We are predicting that a plot of log X will be a straight line of slope – Δ H° / 2.303 R.
The enthalpy change for the first step is obviously the enthalpy of fusion of naphthalene. Since we are assuming that the solutions are ideal, the enthalpy change for the second step is zero (this is the definition of an ideal solution). Thus the enthalpy change for the overall reaction, Δ H° is equals to the enthalpy of fusion of naphthalene,
Δ H°fus we then have a second prediction to check; if we can obtain Δ H° from the temperature dependence data, it should be equal to the directly measured value of Δ H°fus for naphthalene.
It is also very interesting to see what the phase rule indicates about the system we shall study. We have two components and two phases. The number of degrees of freedom is expressed in the term as F = C - P + 2, where F is the variance or the number of degrees of freedom which is able to be varied while the number of phases may remain constant, C is the number of components in the present system, and P is the number of phases present. In this case, F = 2-2+2 = 2, of which one is used up because the pressure in the laboratory does not change. Thus, for any particular composition of the liquid solution, there is only one temperature at which the solid phase and the liquid phase can be in equilibrium since the choice of liquid composition has used up the remaining degree of freedom.
When a solution of liquid cools, the temperature drops almost linearly with time until the point is reached where the solution is saturated with respect to each other. This component then begins to form precipitation and the rate of cooling of the sample changes. If the temperature of such a solution is plotted as a function of time, a plot called a cooling curve is obtained. The intersection point of the straight line extrapolations of the two portions of the cooling curve is a very good estimation of the temperature in which the solid should first begin to appear ideally.
Materials:
Naphthalene, diphenylamine
Apparatus:
Pyrex test tube, thermometer, stopwatch, conical flask, weighing balance, magnetic stirring bar, water bath
Procedure:
1. 1.00g of naphthalene was placed into a pyrex test tube and was heated in a 90°C water bath until all the naphthalene was melted.
2. The test tube was removed and was wiped dry followed by placing it in a conical flask. A thermometer was placed into the molten naphthalene and was stirred while taking temperature reading every 10 or 30 seconds until the naphthalene solidified.
3. The diphenylamine was weighed accurately and was added into naphthalene in which the mixture is about 0.8 mole fractions in naphthalene.
4. The mixture was heated in water bath until it is completely melted.
5. The test tube was removed from water bath and processed as before.
6. The temperature at which the solid appears was recorded.
7. The procedure was repeated for second third and fourth addition of diphenylamine such that the mole fractions of naphthalene are about 0.6, 0.4 and 0.2.
Results and calculations:
Pure naphthalene
Number of mole of pure naphthalene = 1.00g / 128.17 g mol-1
= 7.802 x 10-3 mol
First addition of diphenylamine - 0.8 naphthalene/ diphenylamine mixture
Let X be amount of diphenylamine in naphthalene/ diphenylamine mixture
Number of mole of naphthalene = 1.00g / 128.17 g mol-1
= 7.802 x 10-3 mol
0.8 = 7.802 x 10-3 mol / {7.802 x 10-3 mol + (X/169.23 g mol-1)}
X = 0.33g
Thus, the amount of diphenylamine added to pure naphthalene is 0.33g in order to produce a 0.8 mole fraction of naphthalene in the mixture.
Second addition of diphenylamine - 0.6 naphthalene/ diphenylamine mixture
Let X be amount of diphenylamine in naphthalene/ diphenylamine mixture
Number of mole of naphthalene = 1.00g / 128.17 g mol-1
= 7.802 x 10-3 mol
0.6 = 7.802 x 10-3 mol / {7.802 x 10-3 mol + (X/169.23 g mol-1)}
X = 0.88g
Total amount of diphenylamine present in the mixture is 0.88g, since 0.33g of diphenylamine was added previously, hence
0.88g – 0.33g = 0.55g
Therefore, the amount of diphenylamine added to the mixture is 0.55g in order to produce a 0.6 mole fraction of naphthalene in the mixture.
Third addition of diphenylamine - 0.4 naphthalene/ diphenylamine mixture
Let X be amount of diphenylamine in naphthalene/ diphenylamine mixture
Number of mole of naphthalene = 1.00g / 128.17 g mol-1
= 7.802 x 10-3 mol
0.4 = 7.802 x 10-3 mol / {7.802 x 10-3 mol + (X/169.23 g mol-1)}
X = 1.98g
Total amount of diphenylamine present in the mixture is 1.98g, since 0.88g of diphenylamine was added previously, hence
1.98g – 0.88g = 1.10g
Therefore, the additional amount of diphenylamine required is 1.10g in order to produce a 0.4 mole fraction of naphthalene in the mixture.
Forth addition of diphenylamine - 0.2 naphthalene/ diphenylamine mixture
Let X be amount of diphenylamine in naphthalene/ diphenylamine mixture
Number of mole of naphthalene = 1.00g / 128.17 g mol-1
= 7.802 x 10-3 mol
0.2 = 7.802 x 10-3 mol / {7.802 x 10-3 mol + (X/169.23 g mol-1)}
X = 5.28g
Total amount of diphenylamine present in the mixture is 5.28g, since 1.98g of diphenylamine was added previously, hence
5.28g – 1.98g = 3.30g
Therefore, the additional amount of diphenylamine required is 3.30g in order to produce a 0.2 mole fraction of naphthalene in the mixture.
Table 1 Summary of the amount of diphenylamine added
| Mole fraction of naphthalene in mixture | Sequence of addition | Amount of diphenylamine added (g) |
| 1.0 | - | 0.00 |
| 0.8 | First addition | 0.33 |
| 0.6 | Second addition | 0.55 |
| 0.4 | Third addition | 1.10 |
| 0.2 | Forth addition | 3.30 |
Table 2 Temperature of naphthalene/ diphenylamine solution with different mole fractions at 10 seconds intervals
Let Xnaphthalene be the mole fraction of naphthalene
Note: The highlight column represents the temperature in which the solution started to solidify.
Table 3 Table 2 Temperature of naphthalene/diphenylamine solution with different mole fractions at 30 seconds intervals
Let Xnaphthalene be the mole fraction of naphthalene
Note: The highlight column represents the temperature in which the solution started to solidify.
Graph 1 Cooling curve of pure naphthalene
Graph 2 Cooling curve of 0.8 mole fraction of naphthalene
Graph 3 Cooling curve of naphthalene with 0.6 mole fraction
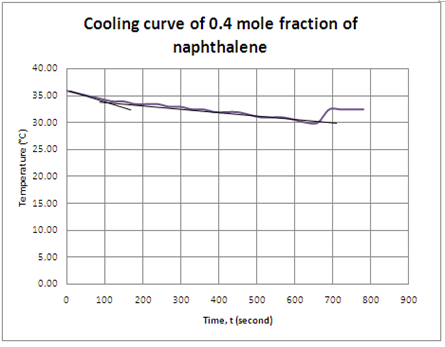
Graph 4 Cooling curve of naphthalene with 0.4 mole fraction
Graph 5 Cooling curve of 0.2 mole fraction of naphthalene
From Graph 1 to Graph 5, the freezing point of each solution has been summarized in the table below.
Table 4 Freezing point of naphthalene with different mole fraction
| Mole fraction of naphthalene, Xnaphthalene
| Freezing point, T (°C) |
| 1.0 | 80.0 |
| 0.8 | 65.0 |
| 0.6 | 52.0 |
| 0.4 | 32.5 |
| 0.2 | 42.0 |
Table 5 and 1/T
| Mole fraction of naphthalene, Xnaphthalene
| Log X | Freezing point, T (K) | 1/T |
| 1.0 | 0.000 | 353.0 | 0.00283 |
| 0.8 | -0.097 | 338.0 | 0.00296 |
| 0.6 | -0.222 | 325.0 | 0.00308 |
| 0.4 | -0.398 | 305.5 | 0.00327 |
| 0.2 | -0.699 | 315.0 | 0.00317 |
From Graph 6, the gradient obtained is -911.1.
The solution is assumed to be ideal solution, so the enthalpy change, is equals to the enthalpy of fusion of naphthalene, .
The relationship between free Gibbs energy, enthalpy and entropy is as follow:
Compared the enthalpy and entropy of naphthalene obtained, the theoretical value of enthalpy and entropy are +18.8kJ mol-1 and +53J mol-1 K-1. The difference between theoretical and experimental value is small, because some of the heat was lost to the surrounding environment.
To find out the molal freezing point depression constant for naphthalene, the formula below is applied:
Thus, the molal freezing point depression constant of naphthalene is 7.69 °C / m.
Discussion:
Freezing point depression is the phenomenon that the freezing point of pure substance falls to lower temperature due to the existence of other impurities. In the other words, the freezing temperature of a solution is lower than the freezing point of pure solvent. This is known as the colligative property of a substance. In this experiment, the diphenylamine is added as the solute into the solvent of naphthalene. The addition of diphenylamine caused the freezing point of naphthalene to go down. . When the solution freezes, the naphthalene solvent and the diphenylamine solidify separately and hence this producing a relatively ordered state. Therefore more energy must be removed to take the solution from its highly disordered liquid state to its ordered solid state than to do the same for pure naphthalene. Hence, solvents with impurities always freeze at a lower temperature than pure solvents.
The naphthalene/diphenylamine solution is not pure and hence the presence of impurities caused the arrangement to be more disordered form when compared to the pure naphthalene. When the impurities (diphenylamine) present in naphthalene, the bonding between naphthalene molecules will be disturbed. The naphthalene molecules are more difficult to form bonding with other molecule and thus the degree of disorder is higher. The bonding of each molecule in this solution is easily to be broken and formed among the molecules. So, the entropy change of naphthalene with impurities has a higher entropy change of pure naphthalene.
From the data obtained, the cooling curve of pure naphthalene showed that the freezing point of this solvent is around 80°C. The pure naphthalene was heated in the water bath at 92°C to melt. From 92°C, the temperature of this solvent kept on dropping until a constant temperature at 80°C. This is known as the freezing point of the solvent. This is because the heat of solvent released is equals to the amount of heat lost to the surrounding. That is why the temperature remained at 80°C. After the solvent is completely solidified (after freezing point), the temperature continues to decrease and stop until room temperature is reached.
For the cases of naphthalene/diphenylamine solution with different mole fraction, the same process was happen in each solution. The cooling curve in each solution showed that freezing point of the solution where the temperature remained constant. However, supercooling was occurs in the cooling process of solution with 0.4 mole fraction of naphthalene. As we can see, the temperature suddenly increased from 30.0°C to 32.5°C at 690th seconds and the temperature kept constant at 32.5°C until 780th seconds. From the observation, the solid is appears at 32.5°C instead of 30.0°C. This is due to the supercooling effect. Supercooling is a phenomenon that describes a solution do not solidify or to form solid but still remain as liquid below its freezing point. Normally, a liquid below its freezing point will crystallize in the presence of a nucleation site in which a crystal structure can form. However, lacking of any such nucleus, the liquid phase can be maintained all the way down to the temperature until crystal homogeneous nucleation occurs.
Theoretically, the freezing point depression in this experiment will be increase as the total amount of diphenylamine present in the solution increase. Based on the data obtained, the freezing point of the solution after first addition, second addition, third addition and forth addition of diphenylamine are 65.0°C, 52.0°C, 32.5°C and 42.0°C respectively. In the three former cases, diphenylamine act as the solute while naphthalene act as solvent in the solution. When the amount of diphenylamine present in the solution is large compared to naphthalene, the role of each other will be shifted. In the case of 0.2 mole fraction of naphthalene, the naphthalene act as solute while diphenylamine act as a solvent in the solution. The solid was appears at 42.0°C is because the freezing point of diphenylamine (solvent) was depressed by the presence of naphthalene (solute).
Precaution steps:
1. The solution must be kept stirred continuously to avoid supercooling effect.
2. The experiment must be performed out of the presence of moving air.
3. The reading of temperature must be taken parallel to the observer’s eyes to avoid parallex error.
4. Do not dispose naphthalene waste into sinks.









No comments:
Post a Comment