Thin Layer Chromatography Technique

Objective:

1. To learn the separation technique by using thin layer chromatography plate in separating a mixture of compounds into individual pure compound

2. To separate the components of maker ink

3. To separate the components of food dye

4. To separate the pigments that present in the spinach via thin later chromatography

Introduction:

The name called chromatography stems from an experiment in which a mixture of coloured (chroma) compounds from a plant extract was separated on paper so that the individual colours were written (graphy) for all to see. Chromatography is one of the most important techniques used in chemistry. It is used to purify desired products from contaminating reaction by products and to isolate biologically active compounds like new drugs from natural sources. Chromatography is also used in chemical analysis. Some examples are the detection of pesticide residues in food, soil and water, prohibited drugs in the blood of athletes and drivers and inorganic ions like nitrate and nitrite whose presence in natural waters can lead to toxic algal blooms.

Chromatography is a common laboratory technique to separate and analyze two or more analytes in the mixture by distribution of two phases: a stationary phase and a mobile phase. The stationary phase is a phase which allows the mobile phase to travel along. These two phases can be solid-liquid, liquid-liquid or gas liquid. This method works on the principle that different compounds with different solubilities and adsorptions to the two phases which they are to be partitioned. The stationary phase bonds to compounds by weak reversible intermolecular interactions (eg. electrostatic, Van der Waals interactions or hydrogen bonding) but most importantly, the strengths of these bonds depend on the structure and polarity of the individual compounds. This is means that when there is a competition between compounds and the bonding sites on the stationary phase some of the compounds will be held more strongly than others.

The compounds in the mobile phase will have different interaction with the polar stationary phase. The factors are mainly depends on the polarity of adsorbent (silica gel in this experiment), solvent polarities, and functional groups of the compounds. The polar adsorbent will more strongly attract the polar molecules of compounds and it will have lower affinity to the non-polar compounds. Hence, the movement of compounds with different polarities could be different. In addition, the polarity of solvent is very important to the compound separations, a solvent system may increase in its polarity by changing the composition of the solvent mixture. The more polar the solvent, the faster the compounds can be drawn up, which means the further the compounds move. The comparison of the polarities of solvent are listed down in the diagram 1.

Diagram 1

The second factor that affects the interaction between stationary phase and compounds is functional group of each compound. The highly polar groups in compound will cause the stronger adsorption and eluted less readily to the stationary phase compared to less polar compounds. Hence, the highly polar compounds will tend to interact strongly with the polar adsorbents and absorb onto the fine particles of the absorbent, hence it travel slowly. The adsorption strengths of each compound having the following types of functional groups in the order of increasing group polarities.

However, the variation may take place which depends on the overall structure of each compound.

In a typical procedure, a mixture of compounds is applied to one end of a plate or column of stationary phase. Then a mobile phase which can carry the compounds in the mixture is allowed to run over or through stationary phase, starting from the end at which the compounds were applied and going to other. As the mobile phase runs, the compounds with strongest bonds to the stationary phase continually displace the others which are then carried further up the chromatography. Consequently, the most weakly bonded molecules end up furthest along the plate and as times goes on, the individual compounds are all separated from each other.

In this experiment, the mixture of the compounds are applied to the bottom of plate or sheet which holding a thin layer of the stationary phase. The mobile phase is allowed to move along the plate by capillary action to develop the chromatography. The compounds are visualized and marked on the plate. In order to visualize the compounds, ordinary visible light is used for coloured compounds, UV light is used for compounds that contain double bonds, and the certain reagent (iodine) is used to react with the separated compounds to produce coloured spots.

Finally, the position of each spot on the plate is measured and reported as the retention factor (or retardation factor), R_f value. Retention factor is the ratio of distance traveled of the compound to the distance of the solvent traveled. Retention factor, R_f is the distance of compound traveled divided by the total distance of solvent travelled in TLC plate. The R_f value are important because they are a consistent property of a compound so long as the stationary and mobile phases are identical. The R_f value can assist in identifying a compound. If two spots travel the same distance on the TLC plate or they have the same retention factor, then both compounds might be concluded as the identical compound.

Materials:

Commercial felt tipped writing pen, spinach, sand, chloroform (CH₂Cl₂), methanol (CH₃OH), petroleum spirit, ethanol (CH₃CH₂OH), 2M ammonia solution, 1-butanol (C₈H₁₀OH), acetone

Apparatus:

Capillary tubes, mortar and pestle, Merck TLC plate, Whatman 12.5cm filter paper, Pasteur pipette, ultra-violet light (long wave length and short wave length)

Procedure:

Part I: Separation of inks from a commercial felt tipped writing pen

Prepare the developing tank

1. 6ml of 1-butanol, 2ml of ethanol and 2ml of 2M ammonia solution were prepared into two 150cm³ beakers.

2. A filter paper was inserted into each beaker and the solution was swirled to wet the paper.

3. Each beaker was covered by a watch glass.

Spot the plate

1. 8.5cm x 3cm of chromatography paper (Whatman SG 81) and 10cm x 3.5cm TLC plate were obtained which can fit inside the developing tank without touching the watch glass.

2. For filter paper and TLC plate, two dots with 1cm apart and 1.2cm from the bottom edge were made by pencil. The dots were labeled as “1” and “2”. The sample (marker ink 500) was spotted on the spot marked “1” once and three times on the spot marked “2”.

3. Steps 1 and 2 were repeated by using marker ink 500A and food dye (red).

Develop the chromatogram

1. The chromatography paper and TLC plate were placed into the different developing tank and make sure that the spots are above the solvent level.

2. The beakers were covered with glass watch.

3. The solvent was allowed to travel upwards.

4. The filter paper and TLC plate were removed and the maximum height of the eluent reached was marked with pencil.

Record the result

1. An accurate drawing was made to show the identity of the sample, the type of stationary phase, the mobile phase, the colour of each discernible spot, the method of visualization and the R_f value for each compound.

Part II: Separation of spinach leaf pigments by TLC

Prepare the developing tank

1. 10ml mobile phase was prepared from the mixture of 9.5ml CH₂Cl₂ and 0.5ml CH₃OH.

2. The mixture was poured into a 150cm³ developing tank.

3. A filter paper was inserted and the mobile phase was swirled to wet the filter paper.

4. The beaker was covered by a watch glass.

Extraction procedure

1. 10g of spinach was grinded by using a mortar and pestle with a portion of sand as extra abrading agent.

2. 20ml of acetone was added and the sample was grinding until the extract is green and the spinach is completely pulped.

3. 10ml petroleum spirit was added and it was mixed quickly with the sample by using pestle.

4. A Pasteur pipette was used to transfer 5ml of the liquid part of the mixture into a 10cm³ glass vial.

5. The vial was capped immediately.

Spot the plate

1. A 1.5cm x 6.6cm TLC plate was used and a dot was made by using a pencil from 1.2cm from the bottom.

2. The green layer of spinach was spotted on the plate several times.

Develop the chromatogram

1. The TLC plate was placed into the developing tank.

2. The solvent front was marked.

Record the result

1. The plate was observed under UV light and the observation was recorded.

2. Accurate drawing of TLC obtained was drawn to show the identity of the sample, the type of stationary phase, the mobile phase, the colour of each discernible spot, the method of visualization and the R_f value for each compound.

Results and calculations:

Based on the formula below to calcuate the retention factor of each component in the sample.

R_f is refers to the retention factor.

Observation:

 

 

 

 

 

 

 

 

 

 

Observation:

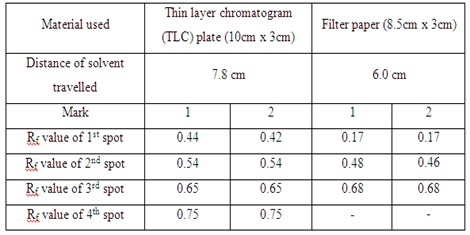
Material used	Thin layer chromatogram (TLC) plate (10cm x 3cm)	Filter paper (8.5cm x 3cm)
Distance of solvent travelled	-	-

Observation:

Observation:

Material used	Thin layer chromatogram (TLC) plate (10cm x 3cm)
Distance of solvent travelled	8.5cm
Rf value of 1st spot	0.09
Rf value of 2nd spot	0.15
Rf value of 3rd spot	0.31
Rf value of 4th spot	0.49

Number of spot	Rf value	Colour observed
1st spot	0.09	Yellow
2nd spot	0.15	Yellow
3rd spot	0.31	Yellow
4th spot	0.49	Green

Discussion:

In the thin layer chromatography, the eluent (solvent) is prepared by using a mixture of 1-butanol, ethanol and ammonia solution in the ratio of 6:2:2. The polarity of the particular solvent cannot be too low because the polar compounds will not be able to carry by the eluent and will not be separated, so that the separation might not be observable. If the solvent of too high polarity is used, the polar compound will travel so fast that the separation between non-polar compound and polar compound to become so small and poor separation will be observed. The solvent mixture is believed that it has the optimized solubility for the organic compounds to dissolve in the solvent. In another word, the compounds can be easily to be carried by the solvent in the TLC plate and filter paper. Before the plate is placed into the solvent, a filter paper was dipped inside the solvent in a beaker which is covered by an evaporating flask. This is to create a system that full with the vapours of organic solvent and hence the solvent is allowed to travel up along the plate faster. After the plate was introduced into the solvent, the solvent start to migrate itself and the compounds move along with solvent until the solvent front has been reached.

There are three components in the chromatography study in which includes the TLC plate with adsorbent or filter paper, the development solvent and the organic compounds that to be analyzed. The adsorbent, silica gel consists of a three dimensional network of thousands of alternating silicon and oxygen bonds. It is a very polar and is capable of hydrogen bonding due to its partial positive charge in silicon and partial negative in oxygen. The silica gel with compete with the development solvent for the organic compounds as the solvent is traveling up through the TLC plate. The silica gel tends to bind the compounds (on stationary phase) while the development solvent tried to dissolve the compounds (on mobile phase) in order to carry the compounds along the plate as the solvent travels up. All the compounds are possible to be adsorbed into the stationary phase however the time of adsorption of compounds in the particular phase is depends on the polarity of each compound. The more polar the compound is, the longer the time taken that the compound adsorbed into the stationary phase so it eluting speed is slower (more time on stationary phase). Less polar compounds are weakly adsorbed, so the time taken for less polar compounds to be adsorbed on stationary phase is shorter. As a result, the less polar compounds can travel further along the plate compared to the more polar compounds. In the paper chromatography, the organic compounds also tend to move upward and the mobile phase carries the organic compounds to run over or through the stationary phase. However, the paper chromatography might not be suitable for some compounds since the compound separation is not good enough in certain case.

In the first part, the food dye (red colour), marker ink 500, and marker ink 500A were used in the study of the chromatography. In the chromatogram a, the food dye were applied one time and three times separately in two different spots (marked as 1 and 2 respectively). The result obtained showed that the distances of each component in food dye moved are almost identical in the TLC plate. This proved that the number of sample spotted on the plate did not affect the distance of each component in food dye travelled in TLC plate. However, the separation of compound in filter paper was not good. This is because there are only three spots appeared on the filter paper (which is shown in chromatogram b) while TLC plate has four single component. In chromatogram c and chromatogram d, there is no spot being observed in both chromatograms. This might be due to the low polarity of sample ink marker 500 in which the low polar organic compounds cannot move in either TLC plate or filter paper. By comparing the chromatogram e and chromatogram f, both chromatograms have one similarity in which they showed that only one component present in the ink marker 500A. Two spots (one spot is being spotted once and another one spot is being spotted three times) in both chromatograms shows the similar R_f value and hence two compounds can be concluded to they migrated the same distance in each chromatogram.

In the second part of the experiment, the spinach was being applied on a TLC plate. The TLC plate showed there are total four components in spinach. The R_f value of the first spot, second spot, third spot, and forth spot are 0.09, 0.15, 0.31, and 0.49 respectively. The colours of each spot in the TLC plate have been recorded, which the compounds with R_f value of 0.09, 0.15 and 0.31 showed yellow colour while the forth spot showed green colour. The yellow spot are predicted as the xanthophylls while the green spot is predicted as chlorophyll. Xanthophylls and chlorophylls are the pigments that usually can be found in the plant

Safety concerns:

1. Always wear goggles and gloves.

2. Handle and dispose the mobile phase into the waste bottle.

3. Do not shake or disturb the mobile phase after TLC plate has been introduced into the beaker.

Solubility Equilibrium

Objective:

1. To study the thermodynamics of solubility of naphthalene in dipheylamine

2. To determine the molal freezing point depression constant of naphthalene

Introduction:

Solubility is the ability of a substance to dissolve in water. The solubility is measured in terms of concentration of an ion that is present in a smaller ratio in solution. On the other hand, solubility equilibrium refers to the equilibrium between the dissolved salt (ions) and undissolved salt that usually exists in a saturated solution or a solution of a sparingly soluble salt.

Naphthalene (pure solid) Naphthalene (solution, mole fraction on X)

The reaction we shall study is the solubility of naphthalene, C₁₀H₈ in diphenylamine, C₁₂H₁₁N, which can be written as the equation shown above. For a saturated solution, the equilibrium constant for this reaction is

K =

Since the activity of a pure solid is unity, so

a_{Naphthalene (solid)}= 1

Assuming that the solution is ideal solution, the activity of naphthalene in the solution is equals to its mole fraction in which a_{Naphthalene (solution)} = X. Therefore, the equilibrium constant is K =X. By the argument of the preceding section, we should predict that the temperature dependence of this solubility equilibrium would be:

= =- [ - ]

The temperature dependence of this equilibrium if found by determining the temperature at which naphthalene first precipitates from liquid mixtures of naphthalene and diphenylamine. This is the temperature at which the mole fraction X in naphthalene solution is saturated with naphthalene. We are predicting that a plot of log X will be a straight line of slope – Δ H° / 2.303 R.

The enthalpy change for the first step is obviously the enthalpy of fusion of naphthalene. Since we are assuming that the solutions are ideal, the enthalpy change for the second step is zero (this is the definition of an ideal solution). Thus the enthalpy change for the overall reaction, Δ H° is equals to the enthalpy of fusion of naphthalene,

Δ H°_fus we then have a second prediction to check; if we can obtain Δ H° from the temperature dependence data, it should be equal to the directly measured value of Δ H°_fus for naphthalene.

It is also very interesting to see what the phase rule indicates about the system we shall study. We have two components and two phases. The number of degrees of freedom is expressed in the term as F = C - P + 2, where F is the variance or the number of degrees of freedom which is able to be varied while the number of phases may remain constant, C is the number of components in the present system, and P is the number of phases present. In this case, F = 2-2+2 = 2, of which one is used up because the pressure in the laboratory does not change. Thus, for any particular composition of the liquid solution, there is only one temperature at which the solid phase and the liquid phase can be in equilibrium since the choice of liquid composition has used up the remaining degree of freedom.

When a solution of liquid cools, the temperature drops almost linearly with time until the point is reached where the solution is saturated with respect to each other. This component then begins to form precipitation and the rate of cooling of the sample changes. If the temperature of such a solution is plotted as a function of time, a plot called a cooling curve is obtained. The intersection point of the straight line extrapolations of the two portions of the cooling curve is a very good estimation of the temperature in which the solid should first begin to appear ideally.

Materials:

Naphthalene, diphenylamine

Apparatus:

Pyrex test tube, thermometer, stopwatch, conical flask, weighing balance, magnetic stirring bar, water bath

Procedure:

1. 1.00g of naphthalene was placed into a pyrex test tube and was heated in a 90°C water bath until all the naphthalene was melted.

2. The test tube was removed and was wiped dry followed by placing it in a conical flask. A thermometer was placed into the molten naphthalene and was stirred while taking temperature reading every 10 or 30 seconds until the naphthalene solidified.

3. The diphenylamine was weighed accurately and was added into naphthalene in which the mixture is about 0.8 mole fractions in naphthalene.

4. The mixture was heated in water bath until it is completely melted.

5. The test tube was removed from water bath and processed as before.

6. The temperature at which the solid appears was recorded.

7. The procedure was repeated for second third and fourth addition of diphenylamine such that the mole fractions of naphthalene are about 0.6, 0.4 and 0.2.

Results and calculations:

Pure naphthalene

Number of mole of pure naphthalene = 1.00g / 128.17 g mol^-1

= 7.802 x 10^-3 mol

First addition of diphenylamine - 0.8 naphthalene/ diphenylamine mixture

Let X be amount of diphenylamine in naphthalene/ diphenylamine mixture

Number of mole of naphthalene = 1.00g / 128.17 g mol^-1

= 7.802 x 10^-3 mol

0.8 = 7.802 x 10^-3 mol / {7.802 x 10^-3 mol + (X/169.23 g mol^-1)}

X = 0.33g

Thus, the amount of diphenylamine added to pure naphthalene is 0.33g in order to produce a 0.8 mole fraction of naphthalene in the mixture.

Second addition of diphenylamine - 0.6 naphthalene/ diphenylamine mixture

Let X be amount of diphenylamine in naphthalene/ diphenylamine mixture

Number of mole of naphthalene = 1.00g / 128.17 g mol^-1

= 7.802 x 10^-3 mol

0.6 = 7.802 x 10^-3 mol / {7.802 x 10^-3 mol + (X/169.23 g mol^-1)}

X = 0.88g

Total amount of diphenylamine present in the mixture is 0.88g, since 0.33g of diphenylamine was added previously, hence

0.88g – 0.33g = 0.55g

Therefore, the amount of diphenylamine added to the mixture is 0.55g in order to produce a 0.6 mole fraction of naphthalene in the mixture.

Third addition of diphenylamine - 0.4 naphthalene/ diphenylamine mixture

Let X be amount of diphenylamine in naphthalene/ diphenylamine mixture

Number of mole of naphthalene = 1.00g / 128.17 g mol^-1

= 7.802 x 10^-3 mol

0.4 = 7.802 x 10^-3 mol / {7.802 x 10^-3 mol + (X/169.23 g mol^-1)}

X = 1.98g

Total amount of diphenylamine present in the mixture is 1.98g, since 0.88g of diphenylamine was added previously, hence

1.98g – 0.88g = 1.10g

Therefore, the additional amount of diphenylamine required is 1.10g in order to produce a 0.4 mole fraction of naphthalene in the mixture.

Forth addition of diphenylamine - 0.2 naphthalene/ diphenylamine mixture

Let X be amount of diphenylamine in naphthalene/ diphenylamine mixture

Number of mole of naphthalene = 1.00g / 128.17 g mol^-1

= 7.802 x 10^-3 mol

0.2 = 7.802 x 10^-3 mol / {7.802 x 10^-3 mol + (X/169.23 g mol^-1)}

X = 5.28g

Total amount of diphenylamine present in the mixture is 5.28g, since 1.98g of diphenylamine was added previously, hence

5.28g – 1.98g = 3.30g

Therefore, the additional amount of diphenylamine required is 3.30g in order to produce a 0.2 mole fraction of naphthalene in the mixture.

Table 1 Summary of the amount of diphenylamine added

Mole fraction of naphthalene in mixture	Sequence of addition	Amount of diphenylamine added (g)
1.0	-	0.00
0.8	First addition	0.33
0.6	Second addition	0.55
0.4	Third addition	1.10
0.2	Forth addition	3.30

Table 2 Temperature of naphthalene/ diphenylamine solution with different mole fractions at 10 seconds intervals

Let X_naphthalene be the mole fraction of naphthalene

Note: The highlight column represents the temperature in which the solution started to solidify.

Table 3 Table 2 Temperature of naphthalene/diphenylamine solution with different mole fractions at 30 seconds intervals

Let X_naphthalene be the mole fraction of naphthalene

Note: The highlight column represents the temperature in which the solution started to solidify.

Graph 1 Cooling curve of pure naphthalene

Graph 2 Cooling curve of 0.8 mole fraction of naphthalene

Graph 3 Cooling curve of naphthalene with 0.6 mole fraction

Graph 4 Cooling curve of naphthalene with 0.4 mole fraction

Graph 5 Cooling curve of 0.2 mole fraction of naphthalene

From Graph 1 to Graph 5, the freezing point of each solution has been summarized in the table below.

Table 4 Freezing point of naphthalene with different mole fraction

Mole fraction of naphthalene, Xnaphthalene	Freezing point, T (°C)
1.0	80.0
0.8	65.0
0.6	52.0
0.4	32.5
0.2	42.0

Table 5 and 1/T

Mole fraction of naphthalene, Xnaphthalene	Log X	Freezing point, T (K)	1/T
1.0	0.000	353.0	0.00283
0.8	-0.097	338.0	0.00296
0.6	-0.222	325.0	0.00308
0.4	-0.398	305.5	0.00327
0.2	-0.699	315.0	0.00317

From Graph 6, the gradient obtained is -911.1.

The solution is assumed to be ideal solution, so the enthalpy change, is equals to the enthalpy of fusion of naphthalene, .

The relationship between free Gibbs energy, enthalpy and entropy is as follow:

Compared the enthalpy and entropy of naphthalene obtained, the theoretical value of enthalpy and entropy are +18.8kJ mol^-1 and +53J mol^-1 K^-1. The difference between theoretical and experimental value is small, because some of the heat was lost to the surrounding environment.

To find out the molal freezing point depression constant for naphthalene, the formula below is applied:

Thus, the molal freezing point depression constant of naphthalene is 7.69 °C / m.

Discussion:

Freezing point depression is the phenomenon that the freezing point of pure substance falls to lower temperature due to the existence of other impurities. In the other words, the freezing temperature of a solution is lower than the freezing point of pure solvent. This is known as the colligative property of a substance. In this experiment, the diphenylamine is added as the solute into the solvent of naphthalene. The addition of diphenylamine caused the freezing point of naphthalene to go down. . When the solution freezes, the naphthalene solvent and the diphenylamine solidify separately and hence this producing a relatively ordered state. Therefore more energy must be removed to take the solution from its highly disordered liquid state to its ordered solid state than to do the same for pure naphthalene. Hence, solvents with impurities always freeze at a lower temperature than pure solvents.

The naphthalene/diphenylamine solution is not pure and hence the presence of impurities caused the arrangement to be more disordered form when compared to the pure naphthalene. When the impurities (diphenylamine) present in naphthalene, the bonding between naphthalene molecules will be disturbed. The naphthalene molecules are more difficult to form bonding with other molecule and thus the degree of disorder is higher. The bonding of each molecule in this solution is easily to be broken and formed among the molecules. So, the entropy change of naphthalene with impurities has a higher entropy change of pure naphthalene.

From the data obtained, the cooling curve of pure naphthalene showed that the freezing point of this solvent is around 80°C. The pure naphthalene was heated in the water bath at 92°C to melt. From 92°C, the temperature of this solvent kept on dropping until a constant temperature at 80°C. This is known as the freezing point of the solvent. This is because the heat of solvent released is equals to the amount of heat lost to the surrounding. That is why the temperature remained at 80°C. After the solvent is completely solidified (after freezing point), the temperature continues to decrease and stop until room temperature is reached.

For the cases of naphthalene/diphenylamine solution with different mole fraction, the same process was happen in each solution. The cooling curve in each solution showed that freezing point of the solution where the temperature remained constant. However, supercooling was occurs in the cooling process of solution with 0.4 mole fraction of naphthalene. As we can see, the temperature suddenly increased from 30.0°C to 32.5°C at 690^th seconds and the temperature kept constant at 32.5°C until 780^th seconds. From the observation, the solid is appears at 32.5°C instead of 30.0°C. This is due to the supercooling effect. Supercooling is a phenomenon that describes a solution do not solidify or to form solid but still remain as liquid below its freezing point. Normally, a liquid below its freezing point will crystallize in the presence of a nucleation site in which a crystal structure can form. However, lacking of any such nucleus, the liquid phase can be maintained all the way down to the temperature until crystal homogeneous nucleation occurs.

Theoretically, the freezing point depression in this experiment will be increase as the total amount of diphenylamine present in the solution increase. Based on the data obtained, the freezing point of the solution after first addition, second addition, third addition and forth addition of diphenylamine are 65.0°C, 52.0°C, 32.5°C and 42.0°C respectively. In the three former cases, diphenylamine act as the solute while naphthalene act as solvent in the solution. When the amount of diphenylamine present in the solution is large compared to naphthalene, the role of each other will be shifted. In the case of 0.2 mole fraction of naphthalene, the naphthalene act as solute while diphenylamine act as a solvent in the solution. The solid was appears at 42.0°C is because the freezing point of diphenylamine (solvent) was depressed by the presence of naphthalene (solute).

Precaution steps:

1. The solution must be kept stirred continuously to avoid supercooling effect.

2. The experiment must be performed out of the presence of moving air.

3. The reading of temperature must be taken parallel to the observer’s eyes to avoid parallex error.

4. Do not dispose naphthalene waste into sinks.

Solvolysis of the salt of a weak acid and a weak base

Objective:

1. To determine the extent of solvolysis of ammonium borate in water by calorimeter

Results and calculation:

Part I: Mixture of sodium hydroxide, NaOH and hydrochloric acid, HCl

Table 1.1 The temperature of mixture and the time taken from beginning

Time taken from beginning, t (s)	Temperature, T (°C)
0.0	26.0
0.5	27.0
3.5	28.0
5.5	28.5
7.5	29.0
10.5	29.0
12.0	29.5
14.5	29.5
16.5	29.5
19.5	30.0
22.0	30.0
25.0	30.0
29.5	30.0
32.0	30.0
34.0	30.0
94.0	30.0
154.0	30.0
214.0	30.0
274.0	30.0
324.0	30.0

Graph 1 Temperature of mixture against time taken from beginning

Table 1.2 Temperature change of mixture caused by neutralization reaction

 

Initial temperature, Ti (°C)	26.0
Final temperature, Tf (°C)	30.0
Change of temperature, ΔT (°C)	4.0

 

Part II: Mixture of sodium hydroxide, NaOH and boric acid, H₃BO₃

Table 2.1 The temperature of mixture and the time taken from beginning

 

Time taken from beginning, t (s)	Temperature, T (°C)
0.0	26.0
5.5	27.0
8.5	28.0
13.0	28.0
14.0	28.0
15.0	28.0
24.0	28.5
32.0	29.0
44.5	29.0
58.0	29.0
62.0	29.0
69.0	29.0
129.0	29.0
189.0	29.0
249.0	29.0
309.0	29.0
369.0	29.0

Graph 2 Temperature of mixture against time taken from beginning

Table 2.2 Temperature change of mixture caused by neutralization reaction

Initial temperature, Ti (°C)	26.0
Final temperature, Tf (°C)	29.0
Change of temperature, ΔT (°C)	3.0

Part III: Mixture of ammonia, NH₄OH and hydrochloric acid, HCl

Table 3.1 The temperature of mixture and the time taken from beginning

Time taken from beginning, t (s)	Temperature, T (°C)
0.0	25.0
2.0	26.5
5.0	27.0
6.0	28.5
8.0	29.0
10.5	29.0
12.5	29.0
15.0	29.0
17.5	29.5
20.0	29.5
23.0	29.5
26.0	30.0
29.5	30.0
33.0	30.0
39.0	30.0
99.0	30.0
159.0	30.0
219.0	30.0
279.0	30.0
339.0	30.0

Graph 3 Temperature of mixture against time taken from beginning

Table 3.2 Temperature change of mixture caused by neutralization reaction

Initial temperature, Ti (°C)	25.0
Final temperature, Tf (°C)	30.0
Change of temperature, ΔT (°C)	5.0

Part IV: Mixture of ammonia, NH₄OH and boric acid, H₃BO₃

Table 4.1 The temperature of mixture and the time taken from beginning

Time taken from beginning, t (s)	Temperature, T (°C)
0.0	25.0
3.5	26.0
7.0	27.0
11.5	27.0
15.5	27.0
18.0	27.0
22.5	27.0
27.5	27.0
33.0	27.0
37.5	27.0
42.0	27.0
47.5	27.0
52.5	27.0
88.0	27.0
148.0	27.0
208.0	27.0
268.0	27.0
328.0	27.0

Graph 4 Temperature of mixture against time taken from beginning

Table 4.2 Temperature change of mixture caused by neutralization reaction

Initial temperature, Ti (°C)	25.0
Final temperature, Tf (°C)	27.0
Change of temperature, ΔT (°C)	2.0

 

Determination of limiting agent in each part

In the reaction for part I, the limiting agent is calculated as shown below:

Therefore, limiting agent in the reaction is NaOH solution.

The limiting agent in each part is determined by using the method as shown in Part I.

Determination of heat capacity of calorimeter

From the enthalpy change, it can be expressed in the term of

-q = (m_solution)(c_solution)(ΔT) + (c_calorimeter )( ΔT)

-(-ΔH )(n) = (m_solution)(c_solution)(ΔT) + (c_calorimeter )( ΔT)

Since -ΔH = -q / n, and ΔH is negative because neutralization is an exothermic reaction.

Assumptions:

Specific heat capacity of calorimeter = 1.0 cal °C^-1 g^-1

Density of solution = 1g cm^-3 (125ml solution = 125g solution)

Part I

In part I, the enthalpy change of a strong base and a strong acid is -13.36 kcal mol^-1.

Number of moles of reaction = 0.04375 mol since limiting agent has 0.04375 mol.

Let ΔH₁ be the enthalpy change of neutralization reaction of part I.

-(-ΔH₁ )(n) = (m_solution)(c_solution)(ΔT) + (c_calorimeter )( ΔT)

-(-13.36x10³ cal mol^-1)(0.04375mol) = (125g)( 1.0 cal °C^-1 g^-1)(4°C) + (c_calorimeter )(4°C)

c_calorimeter = 21.125g °C^-1

Determination of enthalpy change of each reaction

Part II

Based on part I, c_calorimeter = 21.125 cal °C^-1, ΔT = 3°C

Number of moles of reaction = 0.04375 mol since limiting agent has 0.04375 mol.

Let ΔH₂ be the enthalpy change of neutralization reaction of part II.

-(-ΔH₂ )(n) = (m_solution)(c_solution)(ΔT) + (c_calorimeter )( ΔT)

-(-ΔH₂)(0.04375mol) = (125g)( 1.0 cal °C^-1 g^-1)(3°C) + (21.125 cal °C^-1)(3°C)

ΔH₂ = 10.02 kcal mol^-1

Since neutralization is an exothermic process, so ΔH₂ = -10.02 kcal mol^-1.

Part III

Based on part I, c_calorimeter = 21.125 cal °C^-1, ΔT = 5°C

Number of moles of reaction = 0.04375 mol since limiting agent has 0.04375 mol.

Let ΔH₃ be the enthalpy change of neutralization reaction of part III.

-(-ΔH₃ )(n) = (m_solution)(c_solution)(ΔT) + (c_calorimeter )( ΔT)

-(- ΔH₃)(0.04375mol) = (125g)( 1.0 cal °C^-1 g^-1)(5°C) + (21.125 cal °C^-1)(5°C)

ΔH₃ = 16.7 kcal mol^-1

Since neutralization is an exothermic process, so ΔH₃ = -16.7 kcal mol^-1. However, this value is not valid due to certain error. The enthalpy change of the neutralization reaction between a weak base and a strong acid should be less than the reaction between strong acid and strong base.

Part IV

Based on part I, c_calorimeter = 21.125 cal °C^-1, ΔT = 2°C

Number of moles of reaction = 0.04375 mol since limiting agent has 0.04375 mol.

Let ΔH₄ be the enthalpy change of neutralization reaction of part IV.

-(-ΔH₄ )(n) = (m_solution)(c_solution)(ΔT) + (c_calorimeter )( ΔT)

-(- ΔH₄)(0.04375mol) = (125g)( 1.0 cal °C^-1 g^-1)(2°C) + (21.125 cal °C^-1)(2°C)

ΔH₄ = 6.68 kcal mol^-1

Since neutralization is an exothermic process, so ΔH₄ = -6.68 kcal mol^-1.

Determination of enthalpy change of dissociation of H₃BO₃ and NH₃

Assumption: The reaction between weak base and weak acid goes to completion.

By using the ΔH’s value of obtained,

ΔH₄ = ΔH₂ + ΔH₃ – ΔH₁

ΔH₄ = -10.02 kcal mol^-1 + (-16.7 kcal mol^-1) – (-13.36kcal mol^-1)

ΔH₄ = -13.36 kcal mol^-1

The enthalpy change of neutralization between a weak base and a weak acid is -13.36 kcal mol^-1. By comparing to the value calculated, ΔH₄ = -6.68 kcal mol^-1 (from part IV), this value is bigger. According to the reaction between weak base and weak acid, this value is not valid because the expected value should be less than the value obtained in part I, part II and part III. Since the value of ΔH₃ is not valid, therefore the value obtained by using ΔH₄ = ΔH₂ + ΔH₃ – ΔH₁ is no longer valid.

Determination of fraction of the salt ammonium borate reacts with water

Let a be the fraction of ammonium borate salt reacts with water

K_solv = equilibrium constant of solvolysis

a = 1 – a’ = 1 – (ΔH / ΔH₄)

K = a² / (1-a)²

Based on the formula given above, the fraction of ammonium borate salt reacts with water and equilibrium constant of solvolysis were calculated in each part.

For ΔH = -16.7 kcal mol^-1, the value of fraction of the salt ammonium borate reacts with water is negative value which is -0.25. This is an invalid value. Hence, the value of equilibrium constant of solvolysis is not valid too.

Determination of the dissociation constant, K_a for boric acid

From the previous part, the equilibrium constant of solvolysis for part IV is 1.00, and the value of K_w = 1.0 x 10^-14 and K_b = 1.75 x 10^-5. Therefore, the value of K_a of boric acid is calculated as shown below:

1.00 = 1.0 x 10^-14 / (K_a)(1.75 x 10^-5)

K_a = 5.71 x 10^-10

According to the journal article, Perelygin, Yu. P. & D. Yu. Chistyakov (2006). Boric acid. Russian Journal of Applied Chemistry, 79(12), 2041-2042. doi: 10.1134/S1070427206120305. (Dissociation constant of K_a is 7.3 x 10^-10)

The value obtained experimentally is 5.71 x 10^-10 which shows a deviation with the value of K_a obtained via journal article.