Objective:
1. To measure the conductance of potassium chloride, hydrochloric acid, sodium chloride and sodium acetate
2. To determine the dissociation constant of acetic acid
Introduction:
An electrolyte is any substance containing free ions that make the solution to be electrically conductive. Strong electrolyte can dissociate completely in water to form ions while weak electrolyte dissociate partially in water to form its ions. The conductance of solution is depends on the degree of dissociation of electrolyte. The higher the degrees of dissociation of electrolyte, the more ions are produced in the solution, hence the better the conductivity of electrolyte. According to Ohms’ law,
E = I R
where E is the potential difference, I is the current measured and R is the resistance. The term conductance is generally used for dealing with electrolyte and this is defined as the reciprocal of the resistance of the solution. The relationship between resistance and the conductance of the solution is defined as below:
L (ohm-1 or Ω-1) = 1 / R
Once the resistance, R is known, the conductivity or specific conductance (X) may be obtained from
X (Ω-1 cm-1) = d / AR
where d is the distance separation between two electrodes of the measurement cell, A is refers to the area. The cell constant k of the conductivity cell is defined as
k = d/A
and hence
X = kL
The specific conductance, X is the reciprocal of the resistance in ohm of a 1cm of liquid at a specified temperature. The molar conductivity, Λ of an electrolyte solution is defined as:
Λ (Ω-1 mol-1 cm2) = X /C
For weak electrolyte, the increase of molar conductivity with increasing dilution is ascribed to increased dissociation of the electrolyte molecules to free ions. However, a thermodynamic equilibrium exists between the un-dissociated molecules and the ions formed from dissociation. The dissociation degree, α at the given concentration, C is given by
α = Λ / Λo
where Λo is the molar conductivity in the limit of zero concentration or limiting molar conductivity. For strong electrolytes, the molar conductivity is higher than those of weak electrolyte at high concentrations. As the solutions become dilute, the molar conductivities also increase in the case of weak electrolytes but the variation is less steep than for weak electrolytes.
Kohlrausch’s Law states that at time infinite dilution, the molar conductivity of an electrolyte can be expressed as the sum of the contribution from its individual ions.
Λo = Λ+o + Λ-o
where Λ+o and Λ-o are refers to the conductivities of cation and anion at infinite dilution. In this experiment, the molar conductivity of weak electrolyte is determined by using Kohlrausch’s Law.
Given that the molar conductivities of strong electrolyte are expressed as the following:
Alternatively, Λo and the dissociation constant, ka of weak electrolyte may be obtained from the Ostwald dilution law:
Materials:
0.2000M potassium chloride solution, 0.1000M acetic acid, 0.1000M, hydrochloric acid, 0.1000M sodium chloride solution, 0.1000M sodium acetate solution
Apparatus:
Conductivity meter, 100ml dilution flasks, pipette, burette
Procedure:
Part 1: Determination of cell constant
1. The conductance (L) of 0.2000M potassium chloride solution was measured.
2. The cell constant (k) was determined by using equation 6 with the given specific conductance (X) of this solution of 2.768x10-3 ohm-1 cm-1.
Part 2: Measurement of conductance
1. From the solution acetic acid provided, the successive solution with concentration of 0.0500M, 0.0250M, 0.0125M, 0.00312M, 0.00156M and 0.00078M solution were prepared.
2. The conductance of these solutions was measured.
3. The procedure was repeated with hydrochloric acid, sodium chloride, and sodium acetate.
4. The conductance of water used was measured.
5.
Results and calculations:
Part I Determination of Cell Constant
Conductance, L of:
KCl = 30.07 mΩ-1
Distilled water = 0.00 mΩ-1
Specific conductance, X = 2.768 × 10-3 Ω-1 cm-1
Cell constant, k = X / L
= 2.768 mΩ-1 cm-1 / 30.07 mΩ-1
= 0.09205 cm-1
Table 1 Conductance of solutions with different concentration
Table 2 Specific conductance of each solution with different concentration
Table 3 Molar conductivity of each solution with different concentration
By using Kohlrausch’s law, the
Table 4 Degree of dissociation and dissociation constant of CH3COOH at different concentration
| Concentration of CH3COOH (mol dm-3) | Degree of dissociation, α = Λ / Λo | Dissociation constant, ka of CH3COOH |
| 0.10000 | 0.0189 | 3.64 x10-5 |
| 0.05000 | 0.0310 | 4.96 x10-5 |
| 0.02500 | 0.0388 | 3.92 x10-5 |
| 0.01250 | 0.0511 | 3.44 x10-5 |
| 0.00625 | 0.0622 | 2.58 x10-5 |
| 0.00312 | 0.1245 | 4.85 x10-5 |
| 0.00156 | 0.1950 | 7.37 x10-5 |
| 0.00078 | 0.2471 | 6.33 x10-5 |
*degree of dissociation is calculated by using the formula of α = Λ / Λo
*dissociation constant is calculated by using
Average value of dissociation constant, ka
= [(3.64 + 4.96 + 3.92 + 3.44 + 2.58 + 4.85 + 7.37 + 6.33) × 10-5] / 8
= 4.636 × 10-5
| 1 / Λ (Ω cm-2 mol) | CΛ (× 10-3 Ω-1 cm-1) |
| 1.597 | 0.0626 |
| 0.971 | 0.0515 |
| 0.776 | 0.0322 |
| 0.590 | 0.0212 |
| 0.484 | 0.0129 |
| 0.242 | 0.0129 |
| 0.154 | 0.0101 |
| 0.122 | 0.0064 |
Graph of 1/Λ versus CΛ was plotted.
From Graph 4,
Compared to y = mx + c
m = 1/ (ka x Λo2), c = 1 / Λo
1 / Λo = 0.013 Ω cm-2 mol
Λo = 1 / 0.013 Ω cm-2 mol
= 76.92 Ω-1 cm2 mol-1
m = 23 = 1/ (ka x Λo2)
ka = 1/ (76.92)2 (23)
= 7.35 x10-6
Precaution steps:
1. Use distilled water to rinse the electrodes before use.
2. Shake the electrode briefly to ensure that no air bubbles trapped in electrode.
3. Ensure the electrode surface is completely submerged in solution.
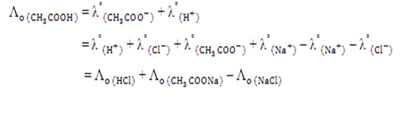

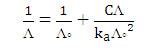
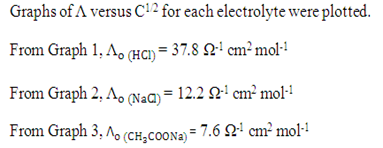



![clip_image002[8] clip_image002[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh6gbe4pinv6Yb_bA4b60YgVt8nhXONoekedTcKufvOJxltZCKlvH-Z64amGaCAPJwc5MB6aZ_h5eZi22k20aCVgwCExFxAKtVO9ovrWjj8b2ZaEahOnlJFxiRRbm5-vL9lfOSg1tIBkDhd/?imgmax=800)









